21.10.25 4주차 알고리즘 - 힙, 트리

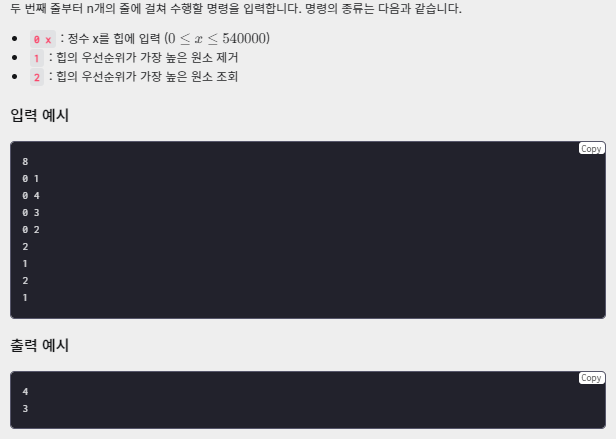
코드

class PriorityQueue:
    '''
    우선순위 큐를 힙으로 구현합니다
    '''
    # 최소 힙 = 부모 < 자식
    def __init__(self) :
        self.data = [0]

    def push(self, value) :
        '''
        우선순위 큐에 value를 삽입합니다.
        '''
        self.data.append(value)
        index = len(self.data) - 1
        # 마지막으로 삽입한 값이 루트노드가 되면 종료.
        while index != 1: #index//2 는 부모노드
            if self.data[index//2]>self.data[index]:
                temp = self.data[index]
                self.data[index] = self.data[index//2]
                self.data[index//2] = temp
                index = index // 2 # 부모와 자식노드를 바꿔준다.
            else : 
                break
    def pop(self) :
        '''
        우선순위가 가장 높은 원소를 제거합니다.
        '''
        if len(self.data) ==1:
            return
        #마지막 노드를 루트 노드 자리로 이동
        self.data[1] = self.data[-1]
        self.data.pop()
        index=1
        while True : 
            priority = -1 # 왼쪽으로 갈지 오른쪽으로 갈지
            #1. 아무 자식도 없는 경우
            if len(self.data) -1 < index * 2:
                break
            elif len(self.data) -1 < index *2 +1: #2.  왼쪽 자식만 있는 경우
                priority=index*2
            else:
                if self.data[index*2]<self.data[index*2 +1]:
                    priority = index*2 # 왼쪽으로 ㄱ
                else:
                    priority = index*2 + 1 # 오른쪽으로 ㄱ
            if self.data[index] > self.data[priority] :
                temp = self.data[index]
                self.data[index]= self.data[priority]
                self.data[priority]=temp
                index = priority
            else:
                break # 이미 최소 힙 조건 충족
        
        
    def top(self) :
        '''
        우선순위가 가장 높은 원소를 반환합니다. 만약 우선순위 큐가 비어있다면 -1을 반환합니다.
        '''
        if len(self.data)==1:
            return -1
        else :
            return self.data[1]

#heapq 라이브러리 사용
import heapq
class PriorityQueue:
    '''
    우선순위 큐를 힙으로 구현합니다
    '''
    # 최소 힙 = 부모 < 자식
    def __init__(self) :
        self.data = []

    def push(self, value) :
        heapq.heappush(self.data,value)
        
    def pop(self) :
        if len(self.data) > 0:
            heapq.heappop(self.data)
        
    def top(self) :
        if len(self.data)==0:
            return -1
        else:
            return self.data[0]

최대힙

import heapq
class PriorityQueue:
    '''
    우선순위 큐를 힙으로 구현합니다
    '''
    # 최대 힙 = 부모 > 자식
    def __init__(self) :
        self.data = []

    def push(self, value) :
        heapq.heappush(self.data,-value) #부호 반전, -5 < -4
        
    def pop(self) :
        if len(self.data) > 0:
            heapq.heappop(self.data)
        
    def top(self) :
        if len(self.data)==0:
            return -1
        else:
            return -self.data[0]

 

절댓값 힙

import heapq
class PriorityQueue:
    '''
    우선순위 큐를 힙으로 구현합니다
    '''

    def __init__(self) :
        self.data = []

    def push(self, value) :
        '''
        우선순위 큐에 value를 삽입합니다.
        '''
        heapq.heappush(self.data, (abs(value), value)) # 튜플 이용

    def pop(self) :
        '''
        우선순위가 가장 높은 원소를 제거합니다.
        '''
        if len(self.data)>0:
            heapq.heappop(self.data)

    def top(self) :
        '''
        우선순위가 가장 높은 원소를 반환합니다. 만약 우선순위 큐가 비어있다면 -1을 반환합니다.
        '''
        if len(self.data)== 0:
            return -1
        else:
            return self.data[0][1] #뒤에 [1]은 튜플의 두번쨰 원소

 

힙 소트

'''
heapSort 함수를 구현하세요.
'''
import heapq
class PriorityQueue:
    '''
    우선순위 큐를 힙으로 구현합니다
    '''
    # 최소 힙 = 부모 < 자식
    def __init__(self) :
        self.data = []

    def push(self, value) :
        heapq.heappush(self.data,value)
        
    def pop(self) :
        if len(self.data) > 0:
            heapq.heappop(self.data)
        
    def top(self) :
        if len(self.data)==0:
            return -1
        else:
            return self.data[0]
            
            
def heapSort(items) :
    '''
    items에 있는 원소를 heap sort하여 리스트로 반환하는 함수를 작성하세요.

    단, 이전에 작성하였던 priorityQueue를 이용하세요.
    '''

    result = []
    
    pq = PriorityQueue()
    
    for item in items:
        pq.push(item)
        
    for i in range(len(items)):
        result.append(pq.top())
        pq.pop()

    return result

 

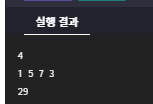
점토 놀이

import heapq

def getMinForce(weights) :
    '''
    n개의 점토를 하나로 합치기 위해 필요한 힘의 합의 최솟값을 반환하는 함수를 작성하세요.
    '''
    pq = []
    for w in weights:
        heapq.heappush(pq,w)
    result = 0
    while len(pq) > 1:
        x = heapq.heappop(pq) # 첫째로 가벼운 점토
        y = heapq.heappop(pq) #둘째로 가벼운 점토
        temp = x+y
        result = result + temp
        
        heapq.heappush(pq, temp) 
        
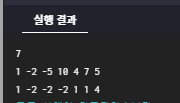
    return result

중간값 출력

import heapq
def find_mid(nums) :
    '''
    n개의 정수들을 담고 있는 배열 nums가 매개변수로 주어집니다.
    nums의 각 정수들이 차례대로 주어질 때, 매 순간마다 
    "지금까지 입력된 수 중에서 중간값"을 리스트로 저장하여 반환하세요.
    '''
    n = len(nums)
    
    result = []
    
    l = [] #최대힙 -l
    r = [] #최소힙 r
    
    for i in range(n):
        x = nums[i]
        
        # l또는 r이 비어있는 경우
        if not l or not r : # l과 r이 처음에 비어있을 때 False로 간주
            heapq.heappush(l,-x)
        else:
            if x >= -l[0] : # x가 l의 루트보다 크다
                heapq.heappush(r,x)
            else:
                heapq.heappush(l,-x)
        # 두 힙의 크기를 조정
        # l과 r은 최대한 전체개수를 반띵하는 갯수로
    
        while not (len(l)==len(r) or len(l)==len(r)+1):
            if len(l) > len(r): # 만약 l이 r보다 2개이상
                heapq.heappush(r, -heapq.heappop(l)) # 반띵을 위해 옮김
            else:
                heapq.heappush(l, -heapq.heappop(r))
        result.append(-l[0])
    
    return result

지금까지 입력한 값의 중간값 출력 > 원래는 매번 정렬해야하나 그러면 n2logn만큼 걸려서 풀 수 X 

그러므로 최소힙을 사용해 왼쪽 최대힙/ 오른쪽 최소힙으로 ( less /중간/ greater)을 이용해 less와 greater의 루트노드를 또 잡아서 비교.